Hypothèse de Riemann, en théorie des nombres, hypothèse du mathématicien allemand Bernhard Riemann concernant l'emplacement des solutions à la fonction zêta de Riemann, qui est connectée au théorème des nombres premiers et a des implications importantes pour la distribution des nombres premiers. Riemann a inclus l'hypothèse dans un article, «Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse» («Sur le nombre de nombres premiers inférieurs à une quantité donnée»), publié dans l'édition de novembre 1859 de Monatsberichte der Berliner Akademie («Revue mensuelle de l'Académie de Berlin »).
La fonction zêta est définie comme la série infinie ζ (s) = 1 + 2 −s + 3 −s + 4 −s + ⋯, ou, en notation plus compacte, , où la sommation (Σ) des termes pour n s'étend de 1 à l'infini en passant par les entiers positifs et s est un entier positif fixe supérieur à 1. La fonction zêta a été étudiée pour la première fois par le mathématicien suisse Leonhard Euler au XVIIIe siècle. (Pour cette raison, elle est parfois appelée la fonction zêta d'Euler. Pour ζ (1), cette série est simplement la série harmonique, connue depuis l'antiquité pour augmenter sans limite, c'est-à-dire que sa somme est infinie.) Euler atteint une renommée instantanée quand il prouvé en 1735 que ζ (2) = π 2 /6, un problème qui avait échappé aux plus grands mathématiciens de l'époque, y compris la famille Bernoulli suisse (Jakob, Johann et Daniel). Plus généralement, Euler a découvert (1739) une relation entre la valeur de la fonction zêta pour les entiers pairs et les nombres de Bernoulli, qui sont les coefficients dans l'expansion de la série Taylor de x / (e x - 1). (Voir aussi fonction exponentielle.) Encore plus étonnant, en 1737, Euler a découvert une formule reliant la fonction zêta, qui implique la somme d'une séquence infinie de termes contenant les entiers positifs, et un produit infini qui implique chaque nombre premier:
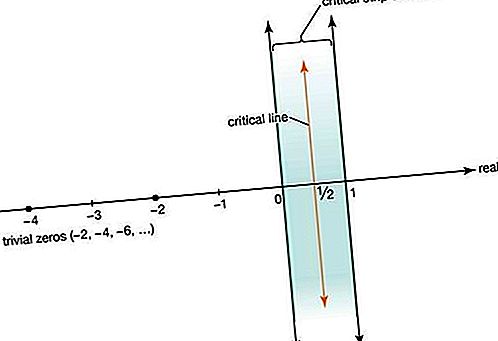
Riemann a étendu l'étude de la fonction zêta pour inclure les nombres complexes x + iy, où i = racine carrée de√ − 1, à l'exception de la ligne x = 1 dans le plan complexe. Riemann savait que la fonction zêta est égale à zéro pour tous les entiers pairs négatifs −2, −4, −6,
(soi-disant zéros triviaux) et qu'il a un nombre infini de zéros dans la bande critique de nombres complexes qui se situent strictement entre les lignes x = 0 et x = 1. Il savait également que tous les zéros non triviaux sont symétriques par rapport à la ligne critique x = une / 2. Riemann a supposé que tous les zéros non triviaux sont sur la ligne critique, une conjecture qui est devenue plus tard connue sous le nom d'hypothèse de Riemann.
En 1914, en anglais mathématicien Godfrey Harold Hardy a prouvé que un nombre infini de solutions de ζ (S) = 0 existent sur la ligne critique x = une / deux. Par la suite, divers mathématiciens ont montré qu'une grande partie des solutions devaient se trouver sur la ligne critique, bien que les fréquentes «preuves» que toutes les solutions non triviales s'y trouvent aient été erronées. Des ordinateurs ont également été utilisés pour tester des solutions, les 10 000 milliards de premières solutions non triviales se trouvant sur la ligne critique.
Une preuve de l'hypothèse de Riemann aurait des conséquences profondes pour la théorie des nombres et pour l'utilisation des nombres premiers en cryptographie.
L'hypothèse de Riemann a longtemps été considérée comme le plus grand problème non résolu en mathématiques. C'était l'un des 10 problèmes mathématiques non résolus (23 dans l'adresse imprimée) présenté comme un défi pour les mathématiciens du 20e siècle par le mathématicien allemand David Hilbert lors du deuxième congrès international de mathématiques à Paris le 8 août 1900. En 2000, le mathématicien américain Stephen Smale a mis à jour l'idée de Hilbert avec une liste de problèmes importants pour le 21e siècle; l'hypothèse de Riemann était numéro un. En 2000, il a été désigné Millenium Problem, l'un des sept problèmes mathématiques sélectionnés par le Clay Mathematics Institute de Cambridge, Mass., États-Unis, pour un prix spécial. La solution pour chaque problème du Millénaire vaut 1 million de dollars. En 2008, la US Defense Advanced Research Projects Agency (DARPA) l'a répertorié comme l'un des défis mathématiques de la DARPA, 23 problèmes mathématiques pour lesquels il sollicitait des propositions de recherche pour un financement - «Mathematical Challenge Nineteen: Settle the Riemann Hypothesis. Le Saint Graal de la théorie des nombres."










![Seconde bataille d'Ypres Première Guerre mondiale [1915] Seconde bataille d'Ypres Première Guerre mondiale [1915]](https://images.thetopknowledge.com/img/world-history/4/second-battle-ypres-world-war-i-1915.jpg)
