Quadrature de la Lune

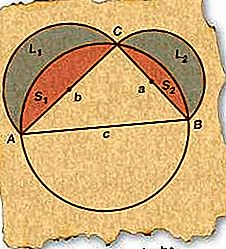
Hippocrate de Chios (fl. C. 460 avant JC) a démontré que les zones en forme de lune entre les arcs de cercle, appelées lunes, pouvaient être exprimées exactement comme une zone rectiligne ou quadrature. Dans le cas simple suivant, deux lunes développées autour des côtés d'un triangle rectangle ont une aire combinée égale à celle du triangle.

1. En commençant par le ΔABC droit, tracez un cercle dont le diamètre coïncide avec AB (côté c), l'hypoténuse. Parce que tout triangle rectangle dessiné avec un diamètre de cercle pour son hypoténuse doit être inscrit dans le cercle, C doit être sur le cercle.

2. Tracez des demi-cercles de diamètres AC (côté b) et BC (côté a) comme sur la figure.

3. Etiqueter les lunes résultantes L ₁ et L ₂ et les segments résultants S ₁ et S ₂, comme indiqué sur la figure.

4. Maintenant, la somme des lunes (L ₁ et L ₂) doit être égale à la somme des demi-cercles (L ₁ + S ₁ et L ₂ + S ₂) les contenant moins les deux segments (S ₁ et S ₂). Ainsi, L ₁ + L ₂ = ^π / ₂ (^b / ₂) ² - S ₁ + ^π / ₂ (^a / ₂) ² - S ₂ (puisque l'aire d'un cercle est π fois le carré du rayon).

5. La somme des segments (S ₁ et S ₂) est égale à l'aire du demi-cercle basée sur AB moins l'aire du triangle. Ainsi, S ₁ + S ₂ = ^π / ₂ (^c / ₂) ² - ΔABC.

6. Substitution de l'expression de l'étape 5 à l'étape 4 et factorisation des termes communs, L ₁ + L ₂ = ^π / ₈ (a ² + b ² - c ²) + ΔABC.

7. Puisque ∠ACB = 90 °, a ² + b ² - c ² = 0, par le théorème de Pythagore. Ainsi, L ₁ + L ₂ = ΔABC.

   Hippocrate a réussi à quadriller plusieurs sortes de lunes, certaines sur des arcs supérieurs et inférieurs aux demi-cercles, et il a laissé entendre, bien qu'il ne l'ait peut-être pas cru, que sa méthode pouvait quadriller un cercle entier. À la fin de l'âge classique, Boethius (v. Ad 470-524), dont les traductions latines d'extraits d'Euclide garderaient la lumière de la géométrie vacillante pendant un demi-millénaire, a mentionné que quelqu'un avait accompli la quadrature du cercle. On ne sait pas si le génie inconnu a utilisé des lunes ou une autre méthode, car, faute d'espace, Boethius n'a pas donné la démonstration. Il a ainsi transmis le défi de la quadrature du cercle avec des fragments de géométrie apparemment utiles pour le réaliser. Les Européens sont restés à la tâche malheureuse jusque dans les Lumières. Enfin, en 1775, l'Académie des sciences de Paris, fatiguée de repérer les erreurs dans les nombreuses solutions qui lui sont soumises, refuse tout autre rapport avec les quadrangristes.