Théorème des nombres premiers, formule qui donne une valeur approximative du nombre de nombres premiers inférieur ou égal à tout nombre réel positif donné x. La notation habituelle pour ce nombre est π (x), de sorte que π (2) = 1, π (3,5) = 2 et π (10) = 4. Le théorème des nombres premiers indique que pour les grandes valeurs de x, π (x) est approximativement égal à x / ln (x). le
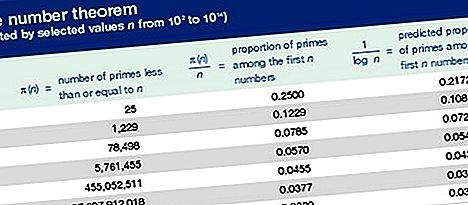
Le tableau compare le nombre réel et prévu de nombres premiers pour différentes valeurs de x.
théorie des nombres: théorème des nombres premiers
L'une des réalisations suprêmes des mathématiques du XIXe siècle a été le théorème des nombres premiers, et il mérite une brève digression. Pour commencer,
Les mathématiciens de la Grèce antique ont été les premiers à étudier les propriétés mathématiques des nombres premiers. (Plus tôt, beaucoup de gens avaient étudié ces nombres pour leurs supposées qualités mystiques ou spirituelles.) Alors que beaucoup de gens ont remarqué que les nombres premiers semblent "s'éclaircir" à mesure que les nombres augmentent, Euclide dans ses Éléments (c. 300 avant JC) peut avoir été le d'abord pour prouver qu'il n'y a pas de plus grand nombre premier; en d'autres termes, il existe une infinité de nombres premiers. Au cours des siècles qui ont suivi, les mathématiciens ont cherché et échoué à trouver une formule avec laquelle ils pourraient produire une séquence sans fin de nombres premiers. A défaut de cette quête d'une formule explicite, d'autres ont commencé à spéculer sur des formules qui pourraient décrire la distribution générale des nombres premiers. Ainsi, le théorème des nombres premiers est apparu pour la première fois en 1798 comme une conjecture du mathématicien français Adrien-Marie Legendre. Sur la base de son étude d'un tableau de nombres premiers jusqu'à 1000000, Legendre a déclaré que si x n'est pas supérieur à 1000000, alors x / (ln (x) - 1,08366) est très proche de π (x). Ce résultat - en fait avec n'importe quelle constante, pas seulement 1.08366 - est essentiellement équivalent au théorème des nombres premiers, qui énonce le résultat pour la constante 0. On sait maintenant, cependant, que la constante qui donne la meilleure approximation de π (x), pour x relativement petit, est 1.
Le grand mathématicien allemand Carl Friedrich Gauss a également conjecturé un équivalent du théorème des nombres premiers dans son cahier, peut-être avant 1800. Cependant, le théorème n'a été prouvé qu'en 1896, lorsque les mathématiciens français Jacques-Salomon Hadamard et Charles de la Valée Poussin indépendamment a montré qu'à la limite (lorsque x augmente à l'infini) le rapport x / ln (x) est égal à π (x).
Bien que le théorème des nombres premiers nous indique que la différence entre π (x) et x / ln (x) devient extrêmement faible par rapport à la taille de l'un ou l'autre de ces nombres lorsque x devient grand, on peut toujours demander une estimation de cette différence. La meilleure estimation de cette différence est supposée être donnée par la racine carrée de√x ln (x).