Section conique, également appelée conique, en géométrie, toute courbe produite par l'intersection d'un plan et d'un cône circulaire droit. Selon l'angle du plan par rapport au cône, l'intersection est un cercle, une ellipse, une hyperbole ou une parabole. Des cas particuliers (dégénérés) d'intersection se produisent lorsque l'avion ne traverse que l'apex (produisant un seul point) ou à travers l'apex et un autre point sur le cône (produisant une ligne droite ou deux lignes droites qui se croisent). Voir la figure.
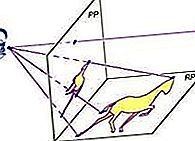
géométrie projective: Sections coniques projectives
Les sections coniques peuvent être considérées comme des sections planes d'un cône circulaire droit (voir la figure). En ce qui concerne
Les descriptions de base, mais pas les noms, des sections coniques peuvent être retracées à Menaechmus (fleuri vers 350 avant JC), élève de Platon et d'Eudoxe de Cnide. Apollonius de Perga (vers 262–190 av. J.-C.), connu sous le nom de «Grand Géomètre», a donné leur nom aux sections coniques et a été le premier à définir les deux branches de l'hyperbole (qui présuppose le double cône). Le traité d'Apollonius en huit volumes sur les sections coniques, Conics, est l'un des plus grands ouvrages scientifiques du monde antique.
Définition analytique
Les coniques peuvent également être décrites comme des courbes planes qui sont les trajectoires (loci) d'un point se déplaçant de telle sorte que le rapport de sa distance d'un point fixe (le foyer) à la distance d'une ligne fixe (la directrice) est une constante, appelée l'excentricité de la courbe. Si l'excentricité est nulle, la courbe est un cercle; si égale à un, une parabole; si moins d'un, une ellipse; et si elle est supérieure à un, une hyperbole. Voir la figure.
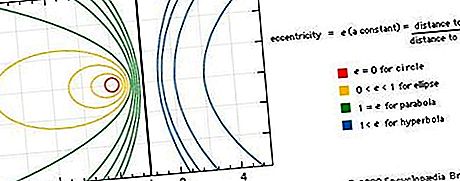
Chaque section conique correspond au graphique d'une équation polynomiale du deuxième degré de la forme Ax 2 + By 2 + 2Cxy + 2Dx + 2Ey + F = 0, où x et y sont des variables et A, B, C, D, E et F sont des coefficients qui dépendent de la conique particulière. Par un choix approprié d'axes de coordonnées, l'équation pour toute conique peut être réduite à l'une des trois formes r simples: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, ou y 2 = 2px, correspondant à une ellipse, une hyperbole et une parabole, respectivement. (Une ellipse où a = b est en fait un cercle.) L'utilisation extensive de systèmes de coordonnées pour l'analyse algébrique des courbes géométriques a commencé avec René Descartes (1596-1650). Voir Histoire de la géométrie: Géométrie cartésienne.
Origines grecques
L'histoire ancienne des sections coniques est jointe au problème du «doublement du cube». Selon Ératosthène de Cyrène (vers 276-190 avant JC), les habitants de Délos ont consulté l'oracle d'Apollon pour obtenir de l'aide pour mettre fin à la peste (vers 430 avant JC) et ont été chargés de construire Apollon un nouvel autel de deux fois le volume de l'ancien autel. et avec la même forme cubique. Perplexe, les Déliens ont consulté Platon, qui a déclaré que «l'oracle signifiait, non pas que le dieu voulait un autel de deux fois la taille, mais qu'il souhaitait, en leur confiant la tâche, faire honte aux Grecs pour leur négligence des mathématiques et leur mépris pour la géométrie. " Hippocrate de Chios (c. 470–410 av. JC) a découvert pour la première fois que le «problème de Délian» pouvait être réduit à trouver deux moyennes proportionnelles entre a et 2a (les volumes des autels respectifs), c'est-à-dire en déterminant x et y de telle sorte qu'un: x = x: y = y: 2a. Ceci revient à résoudre simultanément deux des équations x 2 = ay, y 2 = 2ax et xy = 2a 2, qui correspondent respectivement à deux paraboles et à une hyperbole. Plus tard, Archimède (c. 290–211 avant JC) a montré comment utiliser des sections coniques pour diviser une sphère en deux segments ayant un rapport donné.
Diocle (environ 200 avant JC) a démontré géométriquement que les rayons - par exemple, du Soleil - qui sont parallèles à l'axe d'un paraboloïde de révolution (produits en faisant tourner une parabole autour de son axe de symétrie) se rencontrent au foyer. Archimède aurait utilisé cette propriété pour incendier des navires ennemis. Les propriétés focales de l'ellipse ont été citées par Anthemius de Tralles, l'un des architectes de la cathédrale Sainte-Sophie de Constantinople (achevé en 537), comme un moyen de garantir qu'un autel puisse être illuminé par la lumière du soleil toute la journée.