Analyse tenseur, branche des mathématiques soucieuse des relations ou des lois qui restent valables quel que soit le système de coordonnées utilisé pour spécifier les quantités. Ces relations sont appelées covariantes. Les tenseurs ont été inventés comme une extension des vecteurs pour formaliser la manipulation d'entités géométriques issues de l'étude des variétés mathématiques.
Un vecteur est une entité qui a à la fois une amplitude et une direction; il est représentable par un dessin d'une flèche, et il se combine avec des entités similaires selon la loi du parallélogramme. En raison de cette loi, un vecteur a des composants, un ensemble différent pour chaque système de coordonnées. Lorsque le système de coordonnées est modifié, les composants du vecteur changent selon une loi mathématique de transformation déductible de la loi de parallélogramme. Cette loi de transformation des composants a deux propriétés importantes. Tout d'abord, après une séquence de modifications qui aboutissent dans le système de coordonnées d'origine, les composants du vecteur seront les mêmes qu'au début. Deuxièmement, les relations entre les vecteurs - par exemple, trois vecteurs U, V, W tels que 2U + 5V = 4W - seront présentes dans les composants quel que soit le système de coordonnées.
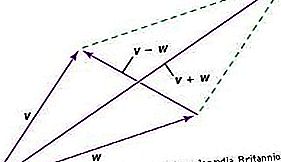
Un vecteur peut donc être considéré comme une entité qui, dans un espace à n dimensions, a n composants qui se transforment selon une loi de transformation spécifique ayant les propriétés ci-dessus. Le vecteur lui-même est une entité objective indépendante des coordonnées, mais il est traité en termes de composants avec tous les systèmes de coordonnées sur un pied d'égalité.
Sans insister sur une image picturale, un tenseur est défini comme une entité objective dont les composants changent selon une loi de transformation qui est une généralisation de la loi de transformation vectorielle mais qui conserve les deux propriétés clés de cette loi. Pour plus de commodité, les coordonnées sont généralement numérotées de 1 à n, et chaque composant d'un tenseur est désigné par une lettre ayant des exposants et des indices, dont chacun prend indépendamment les valeurs 1 à n. Ainsi, un tenseur représenté par les composantes T ab c aurait n 3 composantes comme les valeurs de a, b et c vont de 1 à n. Les scalaires et les vecteurs constituent des cas particuliers de tenseurs, les premiers ne possédant qu'une composante par système de coordonnées et les seconds possédant n. Toute relation linéaire entre les composants du tenseur, telle que 7R a bcd + 2S a bcd - 3T a bcd = 0, si elle est valide dans un système de coordonnées, est valable dans tous et représente donc une relation objective et indépendante des systèmes de coordonnées malgré la absence de représentation picturale.
Deux tenseurs, appelés tenseur métrique et tenseur de courbure, présentent un intérêt particulier. Le tenseur métrique est utilisé, par exemple, pour convertir des composantes vectorielles en amplitudes de vecteurs. Pour plus de simplicité, considérons le cas bidimensionnel avec des coordonnées perpendiculaires simples. Soit le vecteur V ayant les composantes V 1, V 2. Ensuite, par le théorème de Pythagore appliqué au triangle rectangle OAP, le carré de la grandeur de V est donné par OP 2 = (V 1) 2 + (V 2) 2.

Le tenseur métrique cache cette équation. Il est masqué car il se compose ici de 0 et de 1 qui ne sont pas écrits. Si l'équation est réécrite sous la forme OP 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, l'ensemble complet des composants (1, 0, 0, 1) du tenseur métrique est apparent. Si des coordonnées obliques sont utilisées, la formule pour OP 2 prend la forme la plus générale OP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, les quantités g 11, g 12, g 21, g 22 étant les nouveaux composants du tenseur métrique.
À partir du tenseur métrique, il est possible de construire un tenseur complexe, appelé tenseur de courbure, qui représente les différents aspects de la courbure intrinsèque de l'espace à n dimensions auquel il appartient.
Les tenseurs ont de nombreuses applications en géométrie et en physique. En créant sa théorie générale de la relativité, Albert Einstein a soutenu que les lois de la physique doivent être les mêmes quel que soit le système de coordonnées utilisé. Cela l'a amené à exprimer ces lois en termes d'équations tensorielles. Il était déjà connu de sa théorie spéciale de la relativité que le temps et l'espace sont si étroitement liés qu'ils constituent un espace-temps à quatre dimensions indivisible. Einstein a postulé que la gravitation devrait être représentée uniquement en termes du tenseur métrique de l'espace-temps à quatre dimensions. Pour exprimer la loi relativiste de la gravitation, il avait comme blocs de construction le tenseur métrique et le tenseur de courbure formé à partir de celui-ci. Une fois qu'il a décidé de se limiter à ces éléments constitutifs, leur rareté même l'a conduit à une équation tensorielle essentiellement unique pour la loi de la gravitation, dans laquelle la gravitation est apparue non pas comme une force mais comme une manifestation de la courbure de l'espace-temps.
Alors que les tenseurs avaient été étudiés plus tôt, c'est le succès de la théorie générale de la relativité d'Einstein qui a suscité l'intérêt largement répandu des mathématiciens et des physiciens pour les tenseurs et leurs applications.