Permutations et combinaisons, les différentes façons dont les objets d'un ensemble peuvent être sélectionnés, généralement sans remplacement, pour former des sous-ensembles. Cette sélection de sous-ensembles est appelée permutation lorsque l'ordre de sélection est un facteur, une combinaison lorsque l'ordre n'est pas un facteur. En considérant le rapport du nombre de sous-ensembles souhaités au nombre de tous les sous-ensembles possibles pour de nombreux jeux de hasard au XVIIe siècle, les mathématiciens français Blaise Pascal et Pierre de Fermat ont donné une impulsion au développement de la combinatoire et de la théorie des probabilités.
combinatoire: coefficients binomiaux
n objets est appelé permutation de n choses prises r à la fois. Le nombre de permutations est
Les concepts et les différences entre les permutations et les combinaisons peuvent être illustrés en examinant toutes les différentes façons dont une paire d'objets peut être sélectionnée parmi cinq objets distinctifs, tels que les lettres A, B, C, D et E. Si les deux les lettres sélectionnées et l'ordre de sélection sont pris en compte, alors les 20 résultats suivants sont possibles:

Chacune de ces 20 sélections possibles différentes est appelée permutation. En particulier, on les appelle les permutations de cinq objets pris deux à la fois, et le nombre de telles permutations possibles est indiqué par le symbole 5 P 2, lire "5 permute 2". En général, s'il y a n objets disponibles parmi lesquels sélectionner, et si les permutations (P) doivent être formées en utilisant k des objets à la fois, le nombre de permutations différentes possibles est indiqué par le symbole n P k. Une formule pour son évaluation est n P k = n! / (N - k)! L'expression n! - lire «n factoriel» - indique que tous les entiers positifs consécutifs de 1 à n y compris doivent être multipliés ensemble, et 0! est défini comme égal à 1. Par exemple, en utilisant cette formule, le nombre de permutations de cinq objets pris deux à la fois est

(Pour k = n, n P k = n! Ainsi, pour 5 objets il y a 5! = 120 dispositions.)
Pour les combinaisons, k objets sont sélectionnés dans un ensemble de n objets pour produire des sous-ensembles sans ordre. Contrairement à l'exemple de permutation précédent avec la combinaison correspondante, les sous-ensembles AB et BA ne sont plus des sélections distinctes; en éliminant ces cas, il ne reste que 10 sous-ensembles possibles différents: AB, AC, AD, AE, BC, BD, BE, CD, CE et DE.
Le nombre de ces sous-ensembles est désigné par n C k, lire «n choisir k». Pour les combinaisons, puisque k objets ont k! arrangements, il y a k! permutations indiscernables pour chaque choix de k objets; d'où la division de la formule de permutation par k! donne la formule de combinaison suivante:
C'est le même que le coefficient binomial (n, k) (voir théorème binomial). Par exemple, le nombre de combinaisons de cinq objets pris deux à la fois est
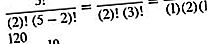
Les formules pour n P k et n C k sont appelées formules de comptage puisqu'elles peuvent être utilisées pour compter le nombre de permutations ou combinaisons possibles dans une situation donnée sans avoir à toutes les énumérer.













